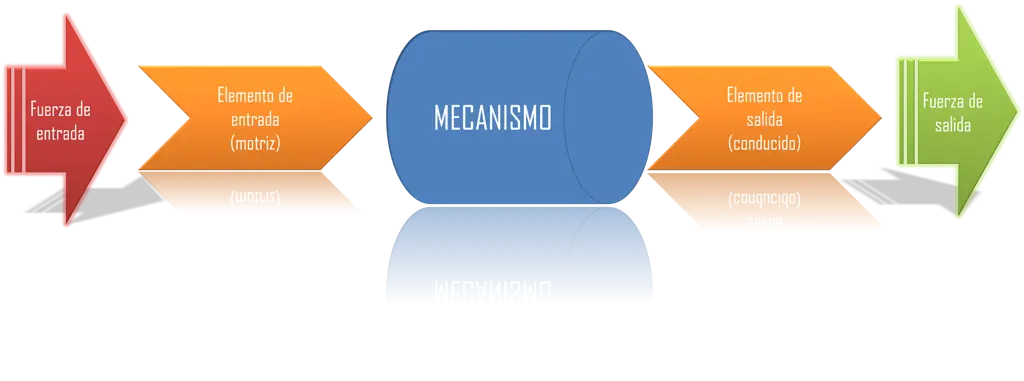
En este blog encontrarás sugerencias relacionadas con componentes y variables que contribuyen a garantizar un funcionamiento preciso de las máquinas. Para ello, conviene recordar algunos aspectos básicos que conforman los sistemas mecánicos de manera esencial:
1. El bloque motriz o bloque de entrada de la fuerza motriz, la cual puede ser de tipo hidráulica, humana, mecánica, etcétera; esta parte es la encargada de poner en marcha el movimiento del sistema mecánico.
2. El bloque transmisor (el mecanismo en sí mismo) es el que recibe, transforma y transmite hacia un elemento de salida tanto el movimiento como las fuerzas provenientes de los dispositivos de entrada.
3. El sistema receptor o sistema de salida está conformado por elementos conducidos que reciben el movimiento y las fuerzas del bloque transmisor; por lo tanto, concreta el trabajo para el cual el sistema mecánico fue concebido.
Asimismo, cabe recordar los dos tipos de movimientos presentes en las aplicaciones:
1.- Movimiento circular o rotatorio que da lugar al torque.
2.- Movimiento lineal cuya magnitud corresponde a la fuerza en newtons.
Ahora bien, sin olvidar los conceptos básicos antes mencionados, toda aplicación que emplea tecnología servo para brindar control de movimiento exige requerimientos específicos de cada uno de sus componentes en cuanto a rendimiento y precisión. En ese sentido, las soluciones sugeridas en este blog tienen como punto de partida dos parámetros que deben formar parte del cálculo llevado a cabo para seleccionar componentes que acompañarán el funcionamiento de algún servomotor.
Juego mecánico
Es el movimiento que tiene lugar en el eje de salida en relación con el eje de entrada fijado, pues se deriva de la holgura que existe entre los engranes de transmisión. En otras palabras, es un error en la posición del eje de salida a causa de un movimiento que lo desfasa con respecto al eje de entrada; la razón de ello es, por ejemplo, que el mecanismo transmisor (como puede ser un reductor de velocidad) presenta espacio libre entre sus dientes de engranaje.
Este efecto también es conocido como holgura y es posible medirlo mediante una fórmula basada en tomar, en ausencia de torque, la rotación en ambas direcciones que existe en la salida de un engranaje reductor mientras el eje de entrada está bloqueado.
Juego mecánico = máxima deflexión – mínima deflexión
ocurridas en 0 Nm de torque
Rigidez torsional
Este concepto se refiere al ángulo de la torsión que sufre el eje debido a fuerzas externas que actúan sobre el reductor o el cople. La rigidez torsional es el cociente obtenido al dividir el torque externo aplicado por el ángulo de giro resultante en la salida del mecanismo reductor. Usualmente, el valor de rigidez torsional es proveído por los fabricantes, aunque es posible medirlo mediante la siguiente fórmula:
Rigidez torsional
=
Torque aplicado
______________________
Deflexión en la salida al aplicar del 5 % al 100 % del torque nominal
Para determinar la rigidez torsional, el reductor es cargado con un torque que continuamente incrementa sobre el torque nominal mientras el eje de entrada está bloqueado. Este efecto también es aplicado en la dirección opuesta. El torque aplicado y el ángulo de deflexión ocurrido en la salida de la brida es medido. Por lo tanto, la rigidez torsional es tomada de la pendiente que presenta la curva de la histéresis entre el 50 y el 100 % del torque nominal. Debido a que la curva es relativamente plana en dicho rango, la rigidez torsional es casi constante.
La siguiente gráfica muestra la curva de la histéresis de un reductor para un torque nominal de + 100 %
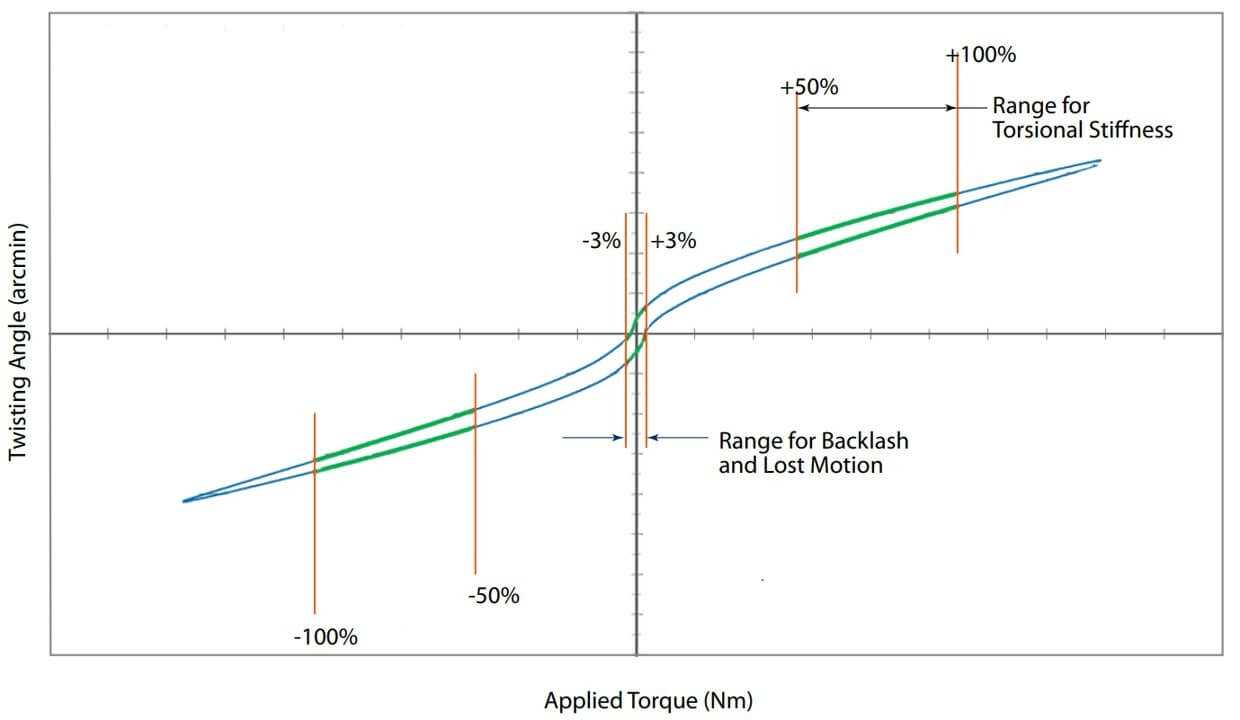
Curva de histéresis de un reductor.
Ahora bien, la rigidez torsional de un sistema completo se calcula al sumar la inversa de la rigidez torsional inversa de cada uno de los componentes. La rigidez torsional total será menor que la de cualquiera de los componentes individuales.
El siguiente ejemplo ilustra el cálculo de la rigidez torsional total a partir de los valores presentados por dos componentes que forman parte de un sistema, cople y reductor.

La rigidez torsional corresponde a la cantidad de torque que un eje radial puede soportar durante su rotación en un sistema mecánico sin que se deforme. La rigidez a la torsión es un parámetro clave para cualquier sistema mecánico que gira sobre un eje fijo. Por lo tanto, su cálculo es vital para comprender la cantidad de tensión que puede soportar un eje giratorio mientras transmite fuerza a través del resto del sistema mecánico.
Efectos derivados del juego mecánico y la rigidez torsional
Pérdida de Movimiento
Combina los efectos del juego mecánico y la rigidez torsional de un mecanismo reductor; al mismo tiempo, depende del torque aplicado. La pérdida de movimiento también es conocida como error de posicionamiento, deflexión resultante de las fuerzas internas del engranaje reductor. Este efecto puede derivarse de la forma en que cada uno de los componentes de la transmisión mecánica están configurados o acomodados. La pérdida de movimiento, pues, también es medida como un ángulo (arcmin).
De forma similar a la rigidez torsional, el mecanismo transmisor es configurado con un torque que incrementa constantemente hasta superar el torque nominal mientras el eje de entrada está bloqueado. Esto es ejecutado también en un sentido contrario. El ángulo de torsión resultante suele ser medido en un +/-3 % del torque nominal, aunque, en la mayoría de casos, es calculado para un valor de torque específico.
Pérdida de movimiento = máxima deflexión – mínima deflexión
en un en un +/-3 % del torque nominal
Prácticamente, la pérdida de movimiento de una aplicación se puede calcular con base en un valor específico de torque aplicado, al sumar la pérdida de movimiento por juego mecánico más la pérdida de movimiento por rigidez torsional. Así, la pérdida de movimiento total puede ser calculada por cada componente y, posteriormente, sumar cada resultado para obtener el valor global.
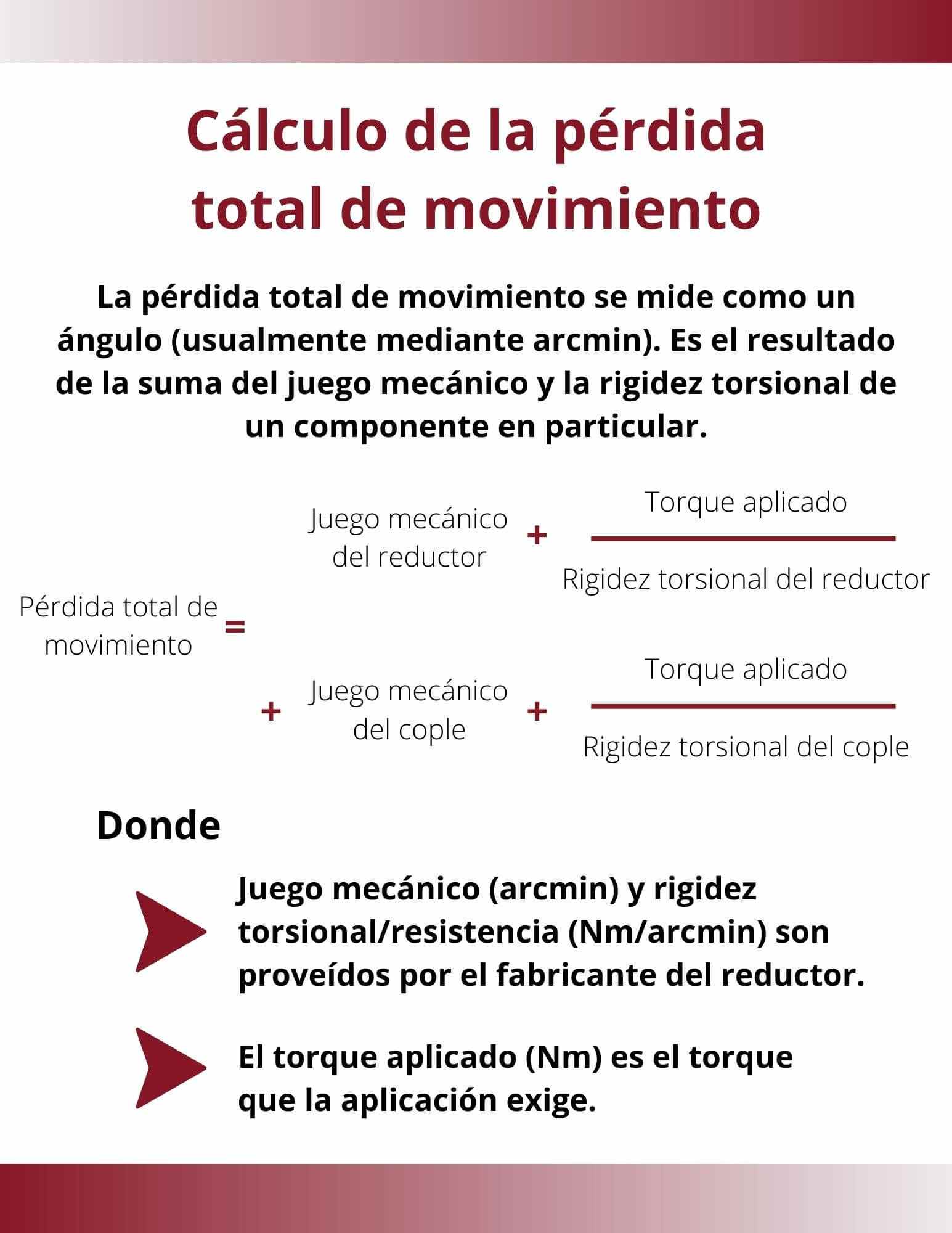
Fórmula para calcular la pérdida total de movimiento.
La pérdida de movimiento puede ser usada como un factor clave al comparar y seleccionar los mejores sistemas de control de movimiento para una aplicación que exige una rigurosa precisión.
Precisión de la transmisión angular
La precisión de la transmisión angular define el error máximo de transmisión ocurrido en la posición de salida real con respecto a la posición de salida teórica según la relación de transmisión. Dado que es el error ocurrido durante el movimiento, muestra de qué manera se acerca el movimiento real a la perfección teórica. Este efecto también es medido como un ángulo (arcsec).
Para medir la precisión de la transmisión angular, el mecanismo reductor es rotado sin carga. Las posiciones de entrada y salida son registradas, pues esto se realiza en múltiples ocasiones y cada dirección. El rango de error ocurrido durante una revolución completa de la posición de salida corresponde al valor de la precisión de la transmisión angular.
Precisión de la transmisión angular =
Variación de la posición máxima – Variación de la posición mínima
La precisión de la transmisión angular es un parámetro clave cuando una aplicación en particular exige precisión durante la rotación y no solo lineal, de extremo a extremo. Un ejemplo de ello son los reductores que formar parte del movimiento de algún robot, pues pueden estar ubicados en alguna de las partes que ejecutan rotaciones. Gracias a una elevada precisión de la transmisión angular, el reductor puede garantizar un movimiento continuo coordinado con el robot.

Pues bien, todos los conceptos anteriores, asociados a la exactitud del movimiento proveniente de elementos como reductores y acoplamientos, repercuten en dos conceptos claves que concretan la calidad de un mecanismo: repetibilidad y posicionamiento. La precisión del posicionamiento es determinada por la diferencia entre la posición que se debe alcanzar y la posición real al que el mecanismo logra llegar. Como tal, el posicionamiento se ve influenciado por la precisión de la transmisión angular, el juego mecánico y la rigidez torsional. Por su parte, la repetibilidad se refiere a la desviación que ocurre cada vez que el reductor regresa a la posición original y con la misma carga.

Posicionamiento con base en el torque nominal.
En la repetibilidad, los errores provenientes de la transmisión angular y la rigidez torsional son constantes, así que cualquier desviación es el resultado de la pérdida de movimiento.
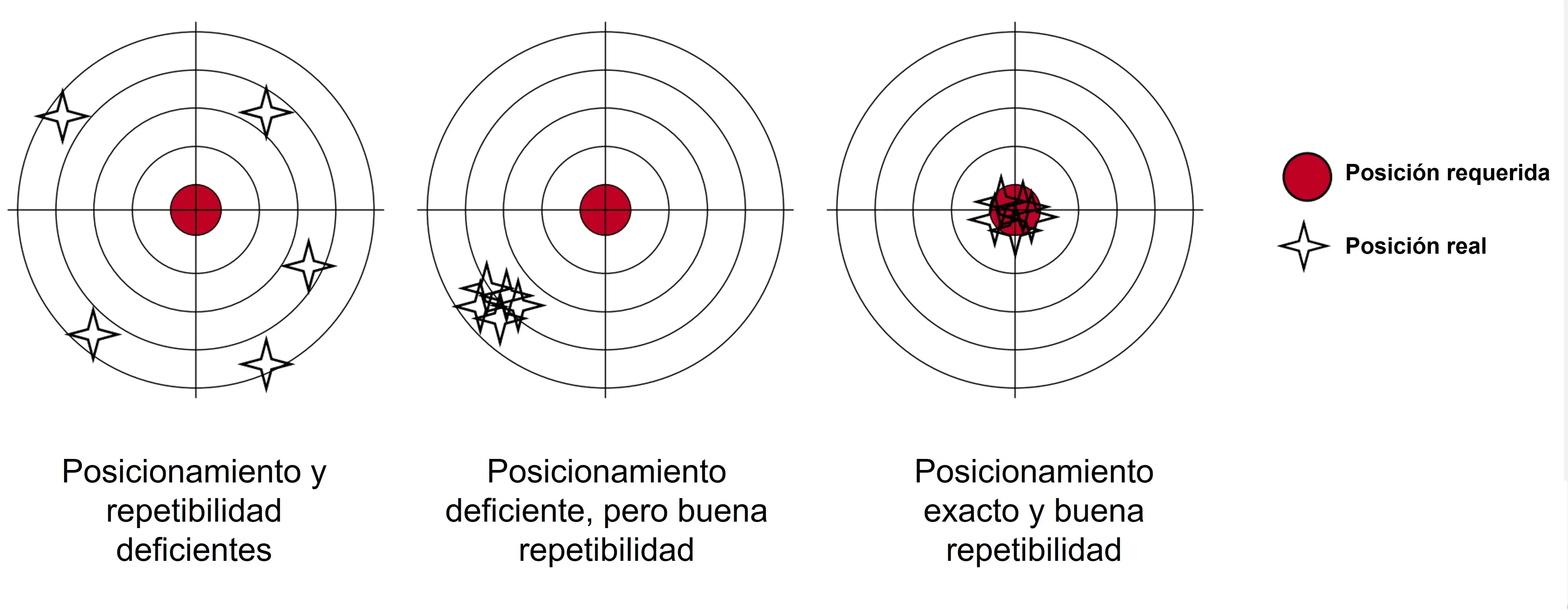
Posicionamiento y repetibilidad.
El juego mecánico permite determinar la precisión de un engranaje reductor. Cuanto menor sea la holgura, mayor será la precisión. Este parámetro, además, se puede combinar con el de la rigidez torsional para determinar la pérdida de movimiento de una aplicación.
Soluciones
En las fórmulas antes explicadas se han dejado entrever dos de los componentes claves para garantizar precisión y excelente rendimiento en una aplicación. La selección precisa de estos, a partir de consideraciones y especificaciones técnicas de la máquina, brindará el éxito de su desempeño mecánico. Tales componentes son los reductores y los acoplamientos.
Los parámetros relacionados con la precisión de un mecanismo pueden acumularse a través de cada uno de los componentes que están en funcionamiento, así que, eliminar o mejorar una pieza son acciones determinantes para optimizar el desempeño de un sistema completo. Por lo tanto, no solo es relevante analizar la pieza y sus dimensiones, sino que también es necesario considerar la tecnología que emplea.
Acoplamientos
Los servocoples pueden estar disponibles con fuelle o con elastómero como tecnologías para acompañar la flecha de salida de un reductor. Pues bien, aunque ambos elementos garantizan cero juego mecánico, el de elastómero presenta menor rigidez torsional y, combinado con un reductor planetario, brinda menor precisión; no obstante, tiene un mejor desempeño en aplicaciones con más vibración. Entonces, a simple vista, un cople de fuelle sería mucho más conveniente. No obstante, también te sugerimos tener presentes algunas preguntas iniciales de las que puedes partir para darte una idea de cuál tecnología sería la ideal para tu aplicación; esto, sin dejar de lado que un riguroso proceso de cálculo de la mano de un experto siempre será la herramienta que te brinde la respuesta más certera.
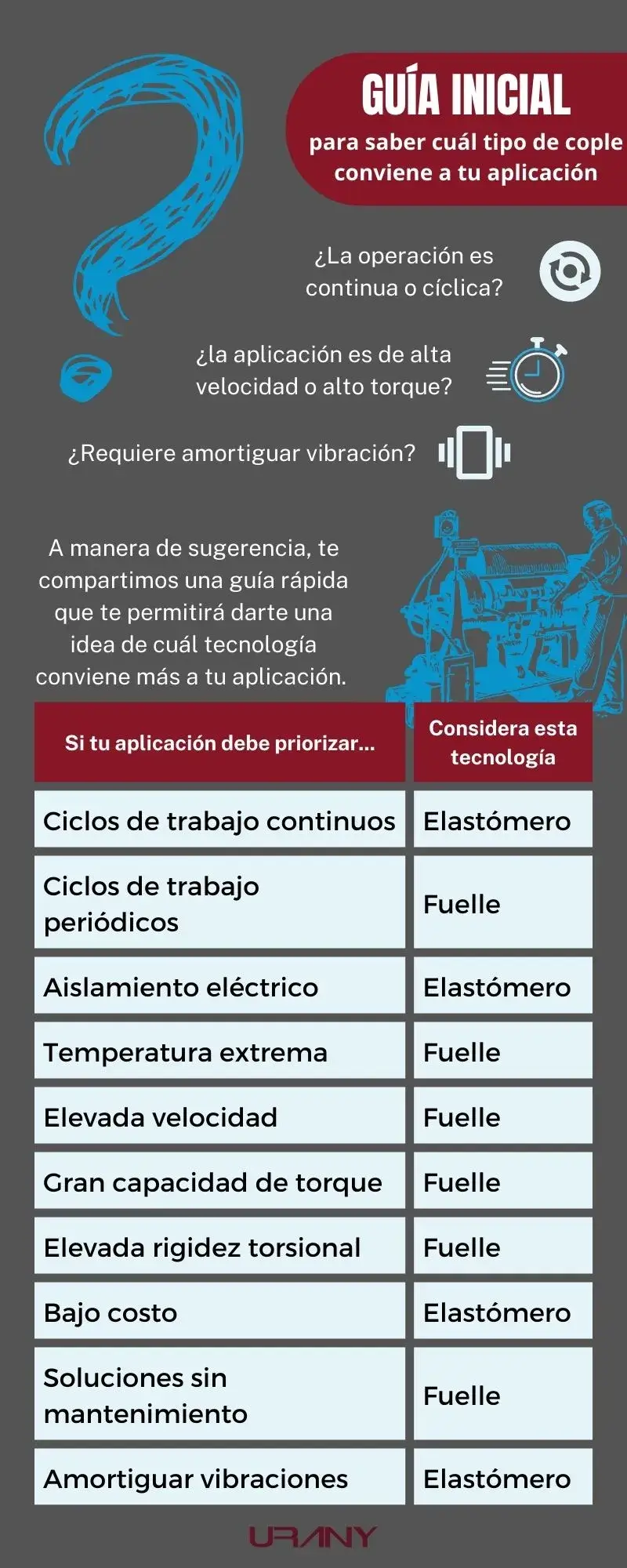
¿Cuál es el cople ideal?
Te interesa leer nuestro blog “Acoplamientos Smartflex, complemento ideal para tu tecnología servo”
Los acoplamiento Smartflex® de fuelle fabricados por mayr® están especialmente diseñados para aplicaciones con servomotor o motor paso a paso; son ideales para servoaccionamientos, así como para accionamientos muy dinámicos con revoluciones elevadas. Además, presentan ventajas asociadas con la flexibilidad, momento de inercia mínimo y excelente capacidad en cuanto a compensación de desalineaciones del eje. En cuanto a precisión y desempeño, están permanentemente libres de holguras y garantizan alta rigidez torsional, lo cual significa que el movimiento de uno de los extremos del eje garantiza el movimiento en el otro extremo con una mínima ventana de error; finalmente, presentan un torque nominal de hasta 700 Nm.
Tamaños disponibles para acoplamientos de fuelle Smartflex®
En Urany tenemos en existencia para entrega inmediada tanto acoplamientos de fuelle como de elastómero; además, contamos con un equipo de expertos que pueden asesorarte con el propósito de adquirir el tamaño y la tecnología ideal para tu aplicación. Mientras, te invitamos a descargar nuestro catálogo de stock para conocer todas las características técnicas de estos componentes fabricados por mayr®.
Reductores
Estos componentes tienen un impacto determinante en la precisión de un sistema que exige especificaciones técnicas superiores. Entre las opciones de engranajes es posible encontrar mecanismos planetarios, hipoidales, cónicos o sinfín-corona con desempeño excelente en cuanto a precisión, densidad de torque y posicionamiento; sin embargo, actualmente, fabricantes reconocidos como Wittenstein también han diseñado tecnologías innovadoras que prescinden de un engranaje clásico para garantizar cero juego mecánico y seis veces más superficie de contacto sobre el eje.
Las soluciones que Wittenstein ofrece en reductores no tienen comparación en el mercado gracias a su relación precio-rendimiento. En cuanto a la transmisión angular, por ejemplo, el destacado desempeño de los reductores DP+ (Línea Advanced) es el preferido para los robots delta; esta línea de reductores presenta un juego mecánico reducido de < 1 a < 2 arcmin, incluso, con un torque máximo de aceleración de hasta 1402 Nm. Estos reductores planetarios representan un excelente ejemplo del desempeño que consiguen los mecanismos fabricados por Wittenstein.

Conocer todas las características de las series Advanced y Premium de los reductores Wittenstein
En cuanto a la tecnología innovadora de Galaxie®, también diseñada y fabricada por Wittenstein, esta ofrece una solución sin igual para conseguir rigidez extrema, cero juego mecánico, menos vibración, capacidad de sobrecarga y hasta un 40 % de aumento en la productividad. Los reductores Galaxie® destacan por su diseño con dientes individuales dinamizados que sustituyen un típico anillo dentado rígido, así como por el contacto tangencial que existe en toda la superficie durante el engrane de los dientes. Así que, Galaxie® no se limita a un único contacto lineal entre rodamientos o dientes.
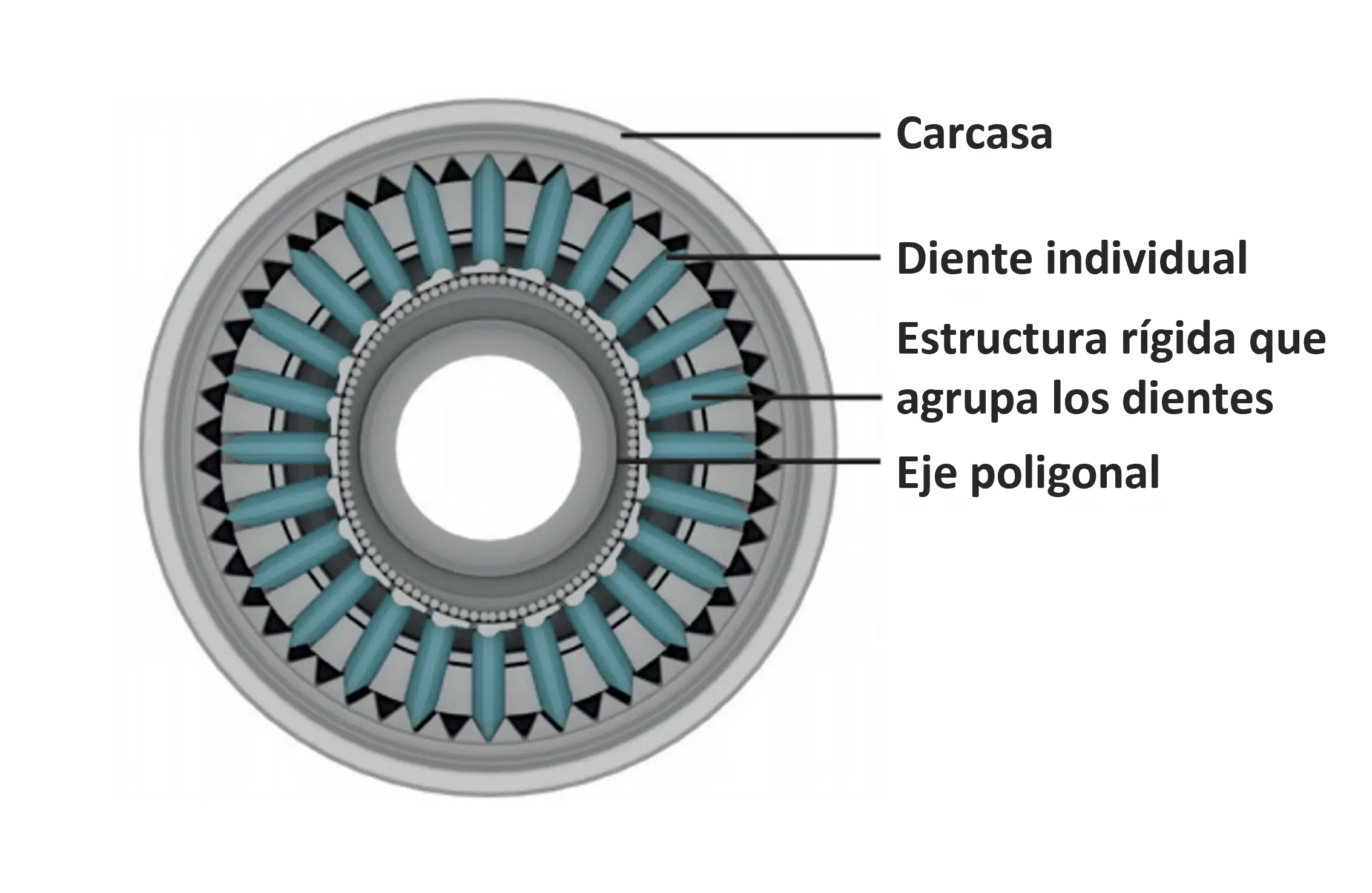
El funcionamiento del reductor Galaxie® se basa en una cinemática en la que los dientes individuales ejercen una fuerza de empuje y, como tal, participan simultáneamente en la transmisión de torque. El diseño de Galaxie® prescinde de un piñón porque realiza la conversión de torque mediante tales dientes, los cuales están agrupados alrededor de un polígono de accionamiento triple, no circular. De esta forma, los dientes individuales son conducidos a lo largo del dentado interior de la corona. Por si fuera poco, el engrane superficial multidiente de este reductor genera una película lubricante, lo cual minimiza el desgaste mecánico y elimina el juego durante toda la vida útil.
¿Soluciones y asesoría personalizada? Encuentra en Urany el componente que buscas para entrega inmediata, así como la tranquilidad de un acompañamiento certero y cercano a las necesidades de tu industria… ¡acércate a nosotros para conocer más o cotizar la solución ideal!